화학공정의 기본이 되는 3가지 공정은 원료의 조제-반응-분리 및 정제이다. 반응 공학은 이 중 반응에 대해 알아보는 학문이다.
CH1:몰 수지와 설계방정식
임의의 화학종 j에 대한 반응기에서의 몰 수지식은 다음과 같다. 몰 수지식이란 j라는 어떤 특정 물질이 반응기에 들어오고 나가고 반응하여 최종적으로 축적되는 양을 나타낸 수지식이다.
보통 유입-유출+생성-소멸=축적량이라는 식으로 알려져 있다. 이는 자명한 식일 것이다. 반응기에 30만큼 들어오고 20만큼 나가고내부에서 생성,소멸된 량이 없다면 축적량은 10인 것이다.
30-20+0-0=10(축적)
이러한 유입-유출+생성-소멸=축적량 식을 수식으로 나타내면 다음과 같다.
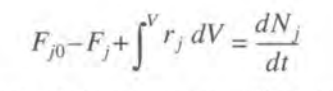
이를 4가지 유형의 반응기(BR,CSTR,PFR,PBR)에 적용 시 다음과 같은 식이 얻어진다.

만약 반응기 각각이 궁금하다면?? 접은글
1. 배치 반응기 (BR, Batch Reactor)
특징:
- 일회성 공정: 반응물이 반응기에 투입되고, 반응이 완료될 때까지 봉쇄된 상태에서 반응이 진행됩니다. 반응이 완료되면 제품을 꺼내고, 다음 공정을 준비합니다.
- 시간 의존성: 반응이 시간에 따라 변화하므로 시간에 따른 농도 변화, 온도 변화 등을 조절하며 반응을 진행합니다.
- 완전 혼합: 반응기 내부에서 반응물이 고르게 혼합된 상태로 반응이 일어납니다.
용도:
- 소규모, 불규칙 생산: 주로 소량의 제품을 만드는 데 적합하며, 제약, 화장품, 특수 화학 제품의 생산에 많이 사용됩니다.
- 연구 및 개발: 새로운 반응 경로를 개발하거나, 최적 반응 조건을 탐색할 때 실험적으로 자주 사용됩니다.
2. 연속 교반탱크 반응기 (CSTR, Continuous Stirred Tank Reactor)
특징:
- 연속적인 반응: 반응물이 일정하게 투입되고, 반응 후 생성물이 지속적으로 배출되는 방식입니다.
- 균일한 혼합: 내부에 교반기가 있어 반응물이 고르게 혼합되므로 반응기 내 농도가 일정합니다.
- 반응속도 낮음: 모든 위치에서 반응물 농도가 동일하여, 반응 속도가 상대적으로 낮습니다.
용도:
- 대규모 생산: 연속적으로 제품을 생산할 수 있기 때문에 대량 생산에 적합하며, 석유화학, 제약, 정유 산업에서 많이 사용됩니다.
- 열에 민감한 반응: 교반이 효율적이기 때문에, 열에 민감한 반응에서 온도 조절이 용이합니다.
3. 관형 반응기 (PFR, Plug Flow Reactor)
특징:
- 관형 구조: 반응기는 길고 좁은 튜브 형태로 되어 있으며, 반응물은 관을 따라 이동하면서 반응이 일어납니다.
- 농도 차이 존재: 반응물은 일정한 속도로 이동하며, 반응기 내부의 위치에 따라 반응물의 농도가 다릅니다. 입구에서 출구로 갈수록 반응물 농도가 감소하고, 생성물 농도는 증가합니다.
- 높은 반응속도: 반응물 농도가 위치에 따라 변동하므로, 초기 반응물 농도가 높은 곳에서 빠르게 반응이 진행됩니다.
용도:
- 연속 대량 생산: 대량 생산에 적합하며, 촉매 반응 및 기체-액체 반응에 주로 사용됩니다.
- 고온 고압 반응: 관형 반응기는 열 및 압력 분포가 일정하게 관리되므로 고온, 고압에서의 반응에 적합합니다.
- 석유화학 산업: 정유, 플라스틱 및 기타 석유 화학 제품의 대량 생산에서 주로 사용됩니다.
4. 포장층 반응기 (PBR, Packed Bed Reactor)
특징:
- 고체 촉매 사용: 반응기 내부에 고체 촉매가 채워져 있으며, 기체 또는 액체 반응물이 이 층을 통과하면서 촉매와 접촉해 반응합니다.
- 비균일 반응: 고체 촉매 표면에서만 반응이 일어나며, 반응물과 촉매 간의 접촉면적이 중요합니다.
- 높은 선택성: 촉매의 성질에 따라 원하는 제품을 선택적으로 생산할 수 있습니다.
용도:
- 촉매 반응: 고체 촉매가 필수인 반응에 사용되며, 석유 정제, 암모니아 합성, 메탄올 생산 등에서 널리 사용됩니다.
- 대용량 기체 반응: 대량의 기체가 필요한 반응, 특히 크래킹이나 수소화 반응 같은 공정에 적합합니다.
이를 예비적 형태의 설계방정식이라고 한다. 이때 반응이 얼만큼 진행되었는지를 나타내는 전화율 X를 도입하면 더 실용적인 식을 얻을 수 있다.

위는 전화율의 정의이다.


전화율을 이용해 NA, FA를 위와 같이 나타낼 수 있으며 이를 예비 설계식에 대입하면 다음과 같은 실용적인 형태의 설계식을 얻게된다.

전화율을 도입한 위 식을 설계식이라고 부르고, 전화율이 도입되지 않은 윗 윗 테이블의 식을 예비 설계식이라고 부르겠다.
이제 반응기의 부피를 산정할 수 있을까? 아쉽게도 적분식에 반응속도 항을 X의 함수로 나타내지 않으면 적분이 불가능하다. 예를 들어 CSTR의 설계식을 가져와보자.
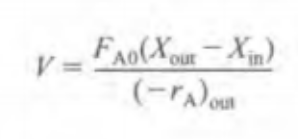
CSTR에서 특정 전화율을 달성하는데 필요한 부피를 산정하기 위해서는, 분자의 조건(초기 유입량, 원하는 전화율)은 알고 있는 상태지만 아래의 -ra(반응속도)는 아직 알지 못한다.
따라서 챕터 3,4에서 반응속도를 전화율 X의 항으로 나타내는 법을 배우도록 한다.
tip) 만약 -ra=f(X)가 주어졌다면, 크기를 산정할 수 있다.
예시를 통해 알아보도록 하자. -ra=f(X) 를 주는 경우는 좀 드물긴 하다.
A->B로 가는 등온 기상 이성질화반응이 있다. 이때 온도는 500K이고 전압은 830kPa이었으며 초기 공급량은 0.4mol이다.
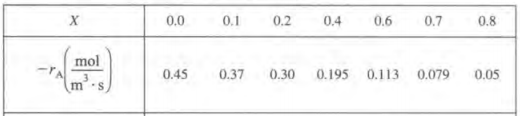
위와 같이 X와 반응속도간의 데이터가 주어지면 특정 전화율을 달성하는데 필요한 V를 구할 수 있다. CSTR또는 PFR이라고 가정시 적분식에는 -1/ra가 들어가므로 위 데이터를 잠시 수정한다.
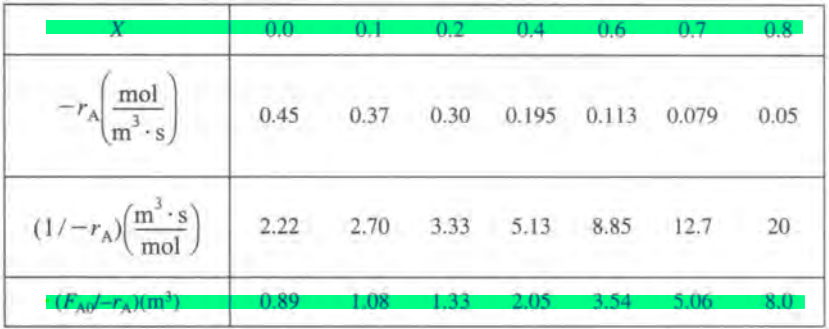
이제 레벤스필 플롯이라고 하는, 전화율 X와 (Fa0/-ra)를 도시하는 그래프를 그려본다.
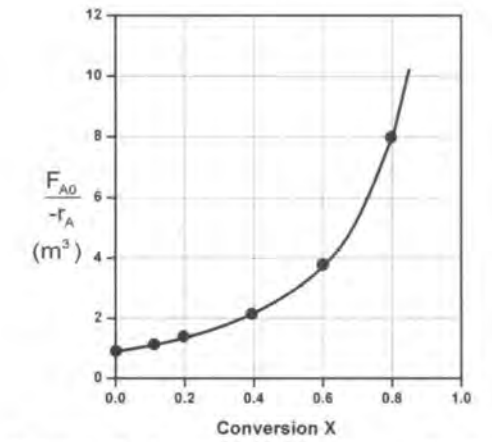
이 그래프의 장점은 특정 전화율을 달성하는 데 필요한 반응기의 부피를 면적으로 보여준다는 것이다. ( 그 이유는 V식을 자세히 보면 알 수 있다.이를 기하적으로 해석한 것이다.)
1)CSTR의 경우 특정 전화율에 해당하는 직사각형 면적이 곧 V이다.
2)PFR의 경우 특정 전화율까지의 곡선 밑의 면적이 V이다.
예를 들어 0.8의 전화율을 달성하는 데 필요한 V를 구해야 한다면
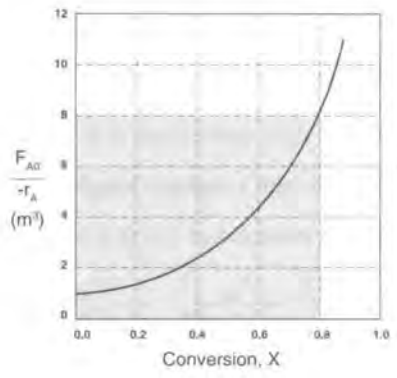
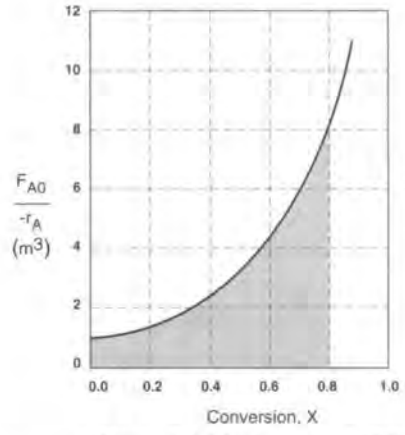
CSTR의 경우 6.4m^3이고 PFR은 2.165m^3임을 알 수 있다.
또는 그냥 반응속도 -ra를 X에 관한 함수로 만들어서 풀 수도 있다. X=0.8을 달성하기 위한 CSTR의 부피는
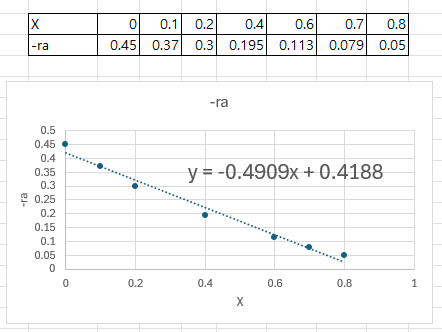
이러면 반응속도 -ra는 -0.4909X+0.4188이다.

설계식에 그냥 때려박아버리자. CSTR의 설계식에 그대로 넣으면 다음과 같다. X=0.8
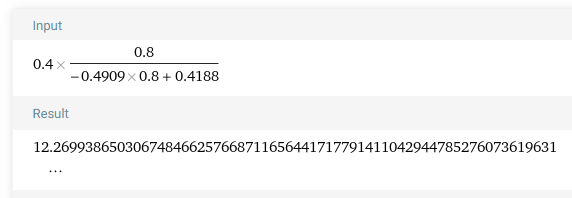
그럼 나오는 부피는 12m^3 인데 위에서 구했던 부피랑 2배차이가 난다! 그 이유는?

그래프를 보면 X=0.8에서 잘 안맞는다.. 대신 X=0.6에서는 똑같은 결과가 나올 것이다.
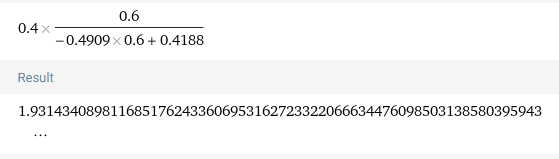
CSTR의 X=0.6일때는 1.93m^3이 나온다.
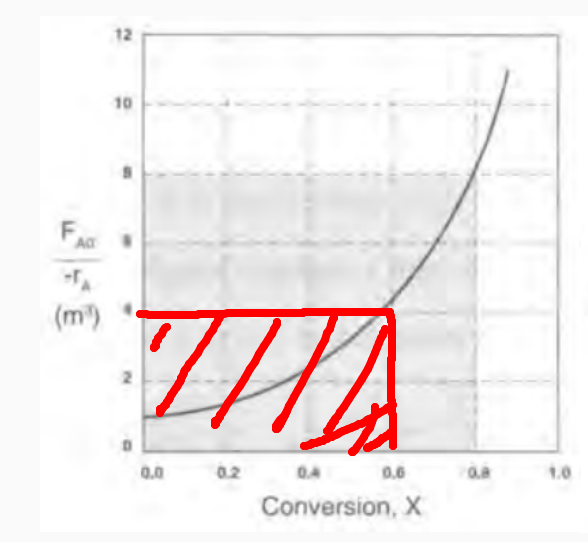

한 2.124쯤 나오므로 대충 맞다고 볼 수 있다.
이제 2단원을 끝내기에 앞서 반응기의 연결을 살펴보자.
많은 경우에 반응기를 하나만 사용하는 것이 아니라 여러개를 직렬로 연결시켜 사용한다. 그 이유는 작은 사이즈 반응기를 여러개 구비해두고 그때 그때 연결하는 것이 큰 반응기 하나를 매번 제조하는 것보다 간단하고 싸기 때문이다.
여러개의 반응기를 연결하는 경우
먼저 Xi를 다음과 같이 정의한다.

이제 CSTR을 직렬로 연결한 경우, PFR을 직렬로 연결한 경우, CSTR과 PFR을 혼합하는 경우를 각각 살펴보자.
Q: 80%의 전화율을 달성하기 위해 2개의 반응기를 연결하려고 한다. 이때 각각의 반응기의 부피는 얼마가 필요한가?
1)CSTR의 직렬연결
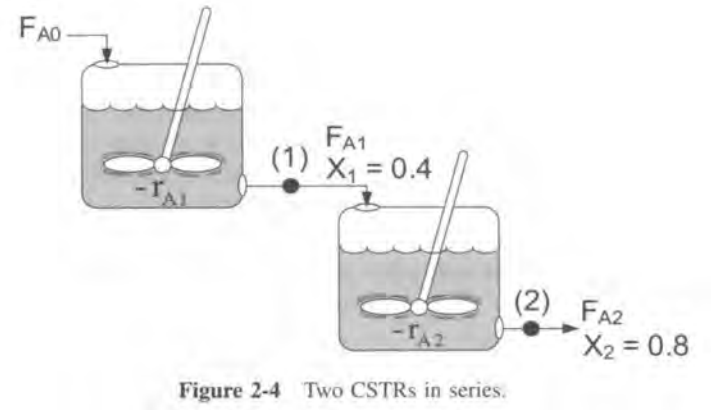


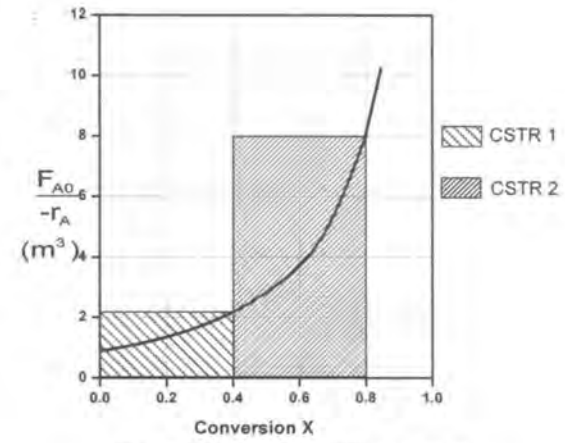
2개를 연결했더니 부피가 줄어든다!
2)PFR의 직렬연결
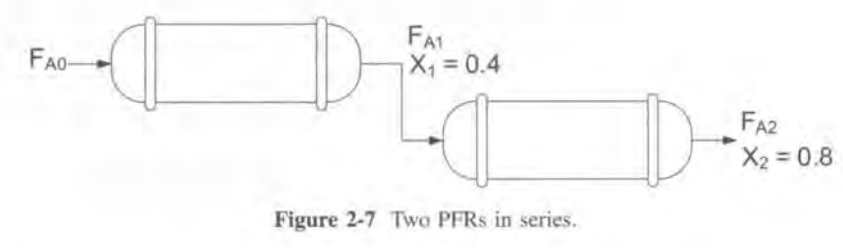
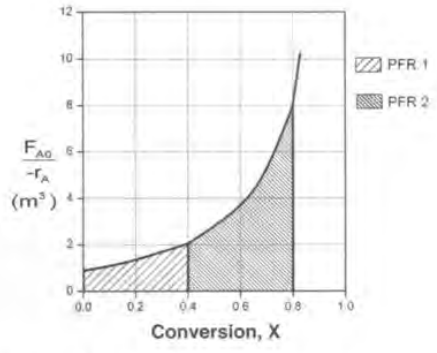
PFR은 딱히 크기가 줄어들진 않는다.
3)CSTR과 PFR을 혼합하면?
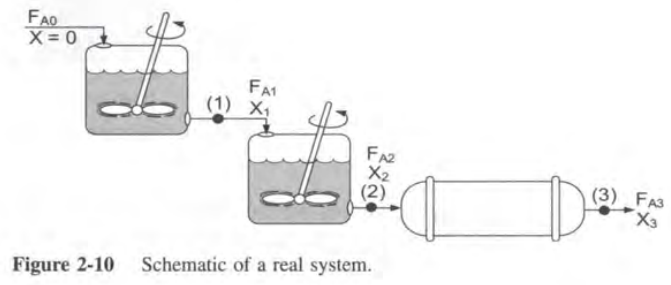
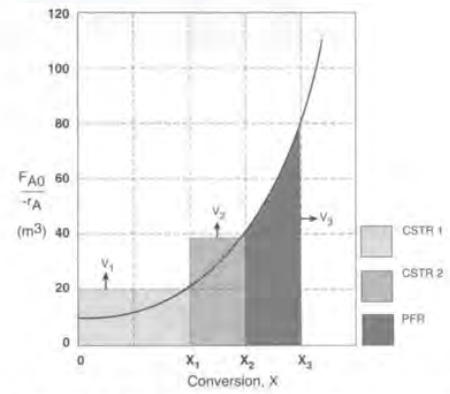
3번째 영역에서 PFR의 하드캐리로 영역이 확 준것을 볼 수 있다! 그냥 CSTR하나 쓰는 것보다 훨씬 작은 부피가 소모된다.
가끔 레벤스필 플롯이 다음처럼 그려질 수도 있다.
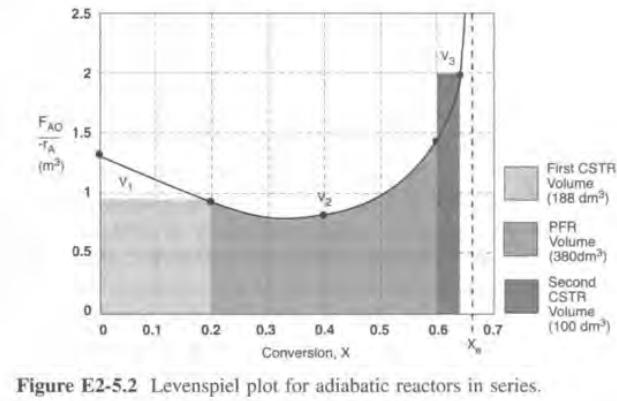
이 경우에는 1번 영역에서 CSTR이 더 경제적이다.
따라서 화공학도는 상황에 따라 반응기의 배치를 결정해볼 수 있을 것이다.
레벤스필도표에 관해서 궁금하다면? 접은글
참고:레벤스필 도표
**레벤스필 도표(Levenspiel Plot)**는 화학반응공학에서 반응기 설계와 성능 분석에 중요한 도구입니다. 이 도표는 주로 **평형 반응기(특히 플러그 흐름 반응기와 CSTR)**의 설계 및 비교에 사용되며, 반응 속도와 반응기의 크기를 시각적으로 분석하는 데 유용합니다.
레벤스필 도표의 기본 개념:
레벤스필 도표는 반응률과 변환율 간의 관계를 나타냅니다. 도표의 기본적인 축은 다음과 같습니다:
- X축: 변환율 X (0 ≤ X ≤ 1), 반응이 얼마나 진행되었는지를 나타냅니다.
- Y축: 반응률의 역수 FA0/−rA, 이는 반응 속도와 반응기 부피의 관계를 시각화하기 위함입니다.
레벤스필 도표를 사용하는 방법:
- CSTR(연속 교반 탱크 반응기):
- CSTR의 부피 계산: CSTR의 경우, 도표에서 특정 변환율 X에서의 반응률 FA0/−rA 값을 읽어 반응기의 부피를 계산합니다.
- 그래프에서 면적: CSTR의 부피는 해당 변환율에서 직사각형 면적으로 표현됩니다.
- PFR(관형 반응기):
- PFR의 부피 계산: PFR의 경우, 반응이 진행되는 동안 반응물의 농도가 연속적으로 변하므로 X의 변화에 따라 그래프 아래 면적을 적분한 값이 반응기의 부피에 해당합니다.
- 그래프에서 면적: PFR의 부피는 곡선 아래의 면적으로 표현되며, ∫FA0/−rAdX로 나타낼 수 있습니다. 즉, 변환율에 따른 면적의 합이 반응기의 총 부피를 나타냅니다.
레벤스필 도표의 해석:
- CSTR vs PFR: 레벤스필 도표를 통해 CSTR과 PFR의 성능을 비교할 수 있습니다. 동일한 변환율을 얻기 위해, CSTR의 경우 PFR보다 더 큰 부피가 필요할 수 있습니다. 이는 CSTR이 반응기 전체에서 반응물 농도가 일정하기 때문에 반응 속도가 낮고, PFR은 반응이 진행될수록 반응물 농도가 낮아지면서 반응 속도가 유지되기 때문입니다.
- 여러 CSTR 연결: CSTR을 직렬로 연결하여 PFR처럼 작동하도록 설계할 수 있습니다. 이때 각 CSTR의 부피는 레벤스필 도표에서 해당 변환율 구간의 면적으로 나타납니다.
응용:
레벤스필 도표는 반응기 설계에서 중요한 요소로, 특정 변환율을 달성하기 위해 필요한 반응기 부피를 쉽게 시각화할 수 있게 해줍니다. 반응기 설계자가 여러 반응기 형태와 조건을 비교하여 최적의 설계를 도출하는 데 매우 유용한 도구입니다.
요약:
- X축: 변환율 X
- Y축: 반응률의 역수 FA0/−rA
- CSTR: 면적은 직사각형으로 나타나며, 일정한 반응 속도를 가집니다.
- PFR: 면적은 곡선 아래의 적분값으로 나타나며, 반응 속도가 변환율에 따라 달라집니다.
레벤스필 도표는 화학반응기 크기와 성능을 예측하는 데 필수적인 시각적 도구입니다.
이제 ch3으로 넘어가 반응속도를 X의 함수로 나타내보자. 먼저 반응속도는 실험을 통해 관찰된다. 가장 흔하게 멱수법칙모델이라고 다음과 같이 주어진다. 가끔 이에 벗어날 수도 있다.
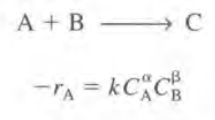
반응속도상수 k는 다음과 같이 주어진다. 상수기는 하지만 온도에 의존하는 값이다.
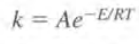
만약 어떤 온도T0에서 k와 E를 알고 있다면 임의의 온도 T에서 속도상수 k를 구할 수 있다.

따라서 반응속도식에서 k는 특정온도에서 상수이므로 농도 (CA,CB)를 X의 함수로 나타낼 수 있다면 대입하여 반응속도를 X로 나타낼 수 있을 것이다. 이는 화학양론표로 구할 수 있다.
농도를 X로 나타내기 step
1)한계반응물을 선정한 후 계수로 반응식을 나눈다.
2)화학양론표를 작성한다.

종, 반응 전 중 후, 토탈 몰 수가 표시된다. 또한 편의를 위해 다음 기호를 정의한다.
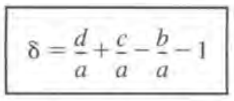
이제 잔존N을 부피V로 나누게 되면 C가 된다.
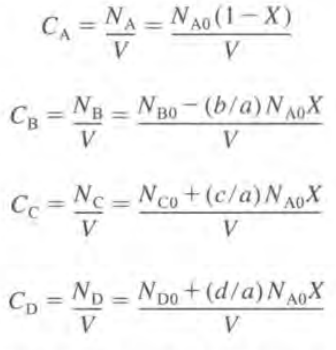
CSTR이면 N이 F로 바뀌고 V는 v로 바뀐다.
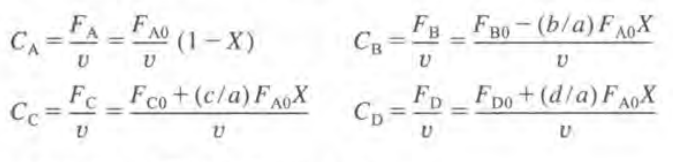
이제 BR과 CSTR에서의 액상반응에서는 부피가 변하지 않으므로, 다음과 같이 쓸 수 있다.
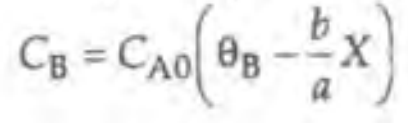
만약 CSTR의 기상반응이라면 V가 변하므로 이러한 접근이 불가능하다. 이때는 다음과 같다.
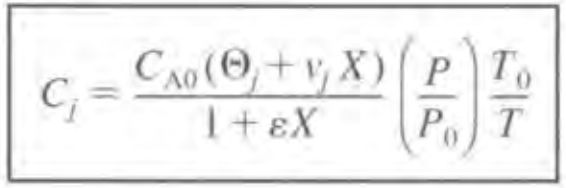
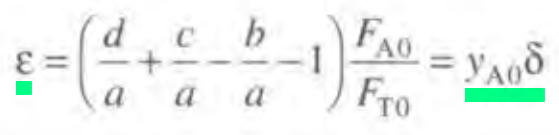
종합하자면 다음과 같다.
이제 설계식을 계산할 수 있게 되었다. 5장에서는 등온 반응기 예제를 살펴보도록 한다.
---------------------------
예제 1: 회분식 반응기에서 반응을 시킨다고 가정할 때, 1차, 2차 반응에서 각기 다른 반응속도상수 k값에 대한 회분식 반응시간을 계산하시오.
먼저 BR의 설계식 표를 가져오자

BR의 미분형태를 가져와 정리하면 다음과 같다. (적분형태를 써도 상관은 없다.)
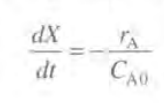
반응을 먼저 2차반응이라고 가정하면 반응식과 속도법칙은 다음과 같다.
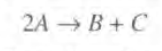
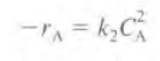
이때 농도 CA는
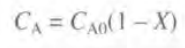
이므로 ra에 대입 후 미분 설계식에 대입 시
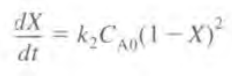
이항 후 적분하면 다음과 같다.
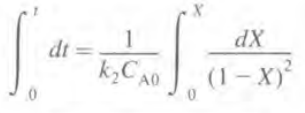
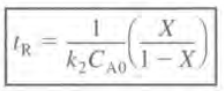
1차 반응도 비슷한 루트로 계산할 경우 반응시간은 다음과 같다.
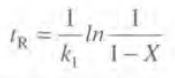
예제를 풀면서 좀 더 알아보자.
예제: 기상반응에 대한 Cj=h(X)구하기
28%SO2와 72% 공기의 혼합물이 흐름 반응기에 주입되어 SO2가 산화된다.
2SO2(g)+O2(g)→2SO3(g)
전압이 1485kPa이고 온도가 500K로 일정할 때 화학양론표를 작성하라.
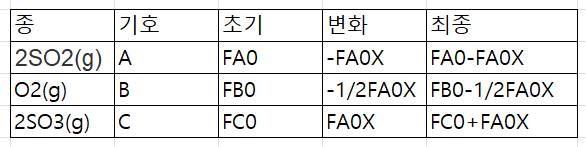
일단 이렇게 화학양론표를 만든다. 이후

여기에 대입하여 농도를 구해본다.
일단 CA0를 구해야 하는데, 여기에 대한 정보는 압력에서 알 수 있다. 압력이 1485kpa인데, 이상기체라고 가정해볼까? 그러면 PV=NRT에서 C=P/RT이다. 그러면 0.28 * 1485kpa / 500k * 8.314 pa*m^3 /mol*K = 0.1mol/dm^3
그러면
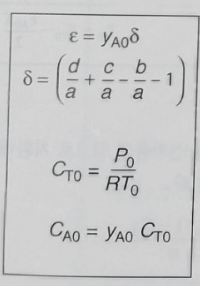
CA0= 0.1
e= 0.28 * (1-1-1/2) =-0.14 (기체 반응이라 yA0= CA0)
이제 대입하면
CA=0.1 (1-X)/(1-0.14X) * P/P0 * T0/T
CB=0.1 (0.54 - 1/2*X)/ (1-0.14X) * P/P0 * T0/T (공기랑 O2는 다른거다! 공기중 21%만이 산소다)
Cc=0.1 (X) / (1-0.14X) * P/P0 * T0/T
이제 P/P0 * T0/T 이거는 1이므로 (온도 압력 일정)
CA=0.1 (1-X)/(1-0.14X)
CB=0.1 (0.54 - 1/2*X)/ (1-0.14X)
Cc=0.1 (X) / (1-0.14X)
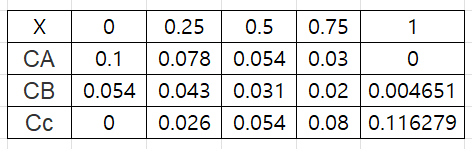
전화율에 따른 농도는 이렇게 된다.
이제 반응속도 -ra를 나타내볼까?
실험적으로 밝혀진 촉매하에서의 SO₂ 산화 반응의 속도 법칙은 보통 아래와 같다:
r=k[SO2][O2]^1/2
따라서
-r = k * 0.1 (1-X)/(1-0.14X) * [ 0.1 (0.54 - 1/2*X)/ (1-0.14X) ]^1/2
이때 k값은 아레니우스 식으로 계산가능하다..

그럼 대충 넣어버리면
-r = 35.7 * 0.1 (1-X)/(1-0.14X) * [ 0.1 (0.54 - 1/2*X)/ (1-0.14X) ]^1/2 /s
이다. 이 식을 통해 FA0/-ra 를 찾고 X에 대한 함수로 나타내어 (레벤스필 도표!)
면적을 구하면 등온 반응기들의 크기를 구할 수 있다.
예제: 평형 전화율의 계산
다음 사산화이질소의 이산화질소로의 가역 기상 분해반응이 등온 등압에서 수행된다.
N2O4(g)⇌2NO2(g)
원료는 340K, 202.6kpa의 순수한 N2O4이다. 340K에서 농도 평형 상수 Kc는 0.1mol/dm^3이다.
a)정용회분식 반응기에서 N2O4의 평형 전화율을 구하여라
b)흐름반응기에서 N2O4의 평형전화율을 구하여라
c)기초반응이라 가정하고, 흐름계와 회분식계의 속도식을 각각 전화율만의 함수로 나타내어라.
d)평형 전화율의 80%를 달성하는데 필요한 CSTR의 부피는?
풀이
a) 정용회분식 반응기에서 N2O4의 평형 전화율을 구하여라
일단 가역반응이니까 당연히 평형 상수 Kc에 대한 식을 세운다.
Kc=CB^2/CA (평형일 때)
이제 표를 만들면 다음과 같다.

이제 만약에 정용회분식이면 부피는 고정이므로
CA=CA0-CA0X
CB=2CA0X
인거고 CA0만 구하면 된다. CA0는 이상기체 방정식 PV=NRT에서 P/RT=202.6kpa/8,314pa m^3/mol k * 340k
CA0 = 0.07167 mol/dm³
CA=CA0-CA0X
CB=2CA0X
CB=0.14334X

대충 풀면 X= 0.441414가 나오고 이게 평형일때 전화율 X이다.
b)흐름반응기에서 N2O4의 평형전화율을 구하여라
이제 흐름 반응기면 V가 좀 복잡하다..


CA=CA0(1-X) / 1+ex
CB=2CA0X / 1+ex
이제 평형식에 대입해보자.
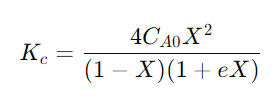
0.1= 4* 0.07167* X^2 /((1-X)(1+X))
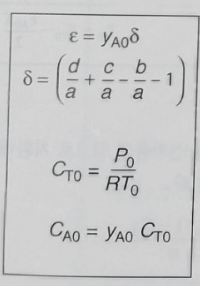
맨 첫줄 식에 의해 e값은 1나온다. 순수한 N2O4이므로 분율은1이고 이때 델타값은 (2-1)
울프람 알파 돌리면 X= 0.508539 정도 나온다
여기서 주의할 점은 평형전화율이 CSTR이 회분식보다 더 크다는 거다. 이건 이제 반응물이 제거가 되면서 발생하는 현상일거다. 회분식은 결과물이 그대로 남아있지만 CSTR은 결과물이 나가면서 제거되어 평형이 오른쪽으로 이동한다.
c)기초반응이라 가정하고, 흐름계와 회분식계의 속도식을 각각 전화율만의 함수로 나타내어라.
음 기초 반응이면 -ra= k(CA - CB^2/K ) 이렇게 된다! 그 이유는 소모도 되지만 역반응으로 생성도 되기 때문에.. 이 식에 이제 배치리액터에서의 농도, CSTR에서의 농도식을 대입만 하면 된다..
CB=0.14334X
(흐름식에서 농도)
CA=CA0(1-X) / 1+ex
CB=2CA0X / 1+ex
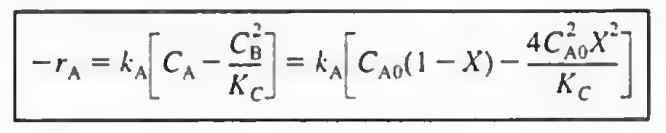
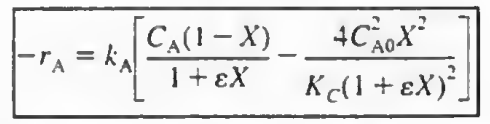
일단 이 두식은 당연히 다르다. 이제 CA0와 평형상수 KC, e=1등등을 대입하면 X에 대한 함수가 된다. 일단 흐름계 CSTR(밑의 식) 에만 대입해서 간단히 정리해보자.
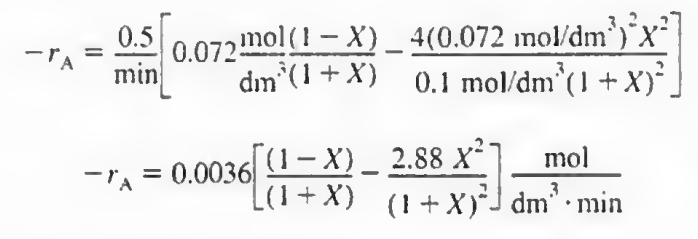
이제 반응기 부피 산정을 위해 레벤스필 도표를 그려보자. 역수를 취해서 그려내면 다음과 같다.
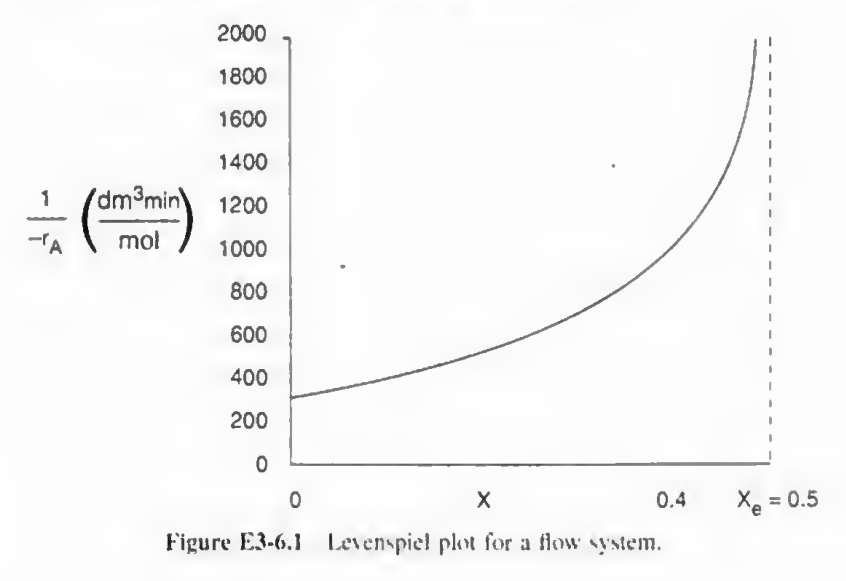
d)평형 전화율의 80%를 달성하는데 필요한 CSTR의 부피는?
일단 평형전화율의 80%는 X=0.4이다.
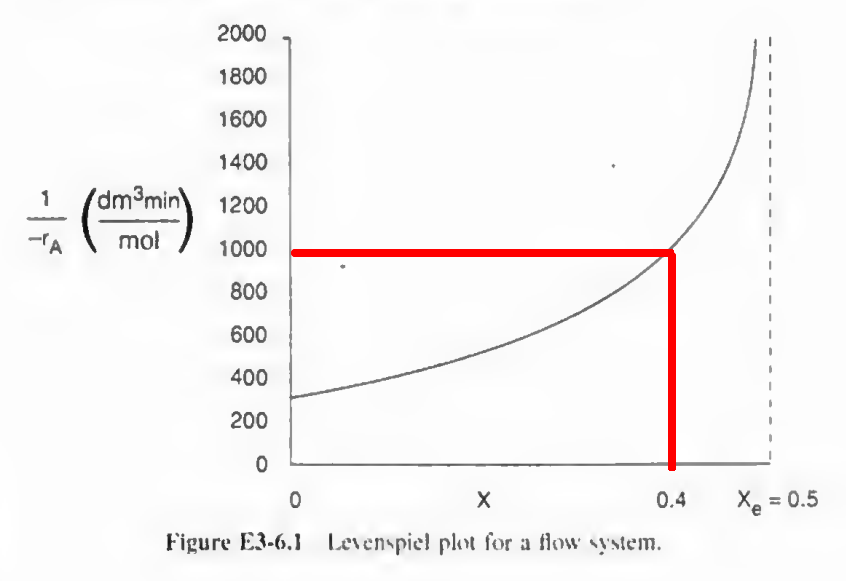
한 1000쯤 된다치면... 1000*0.4*3=1200dm^3 정도 된다. 눈대중이라 제대로 계산하려면 수식을 써야된다.
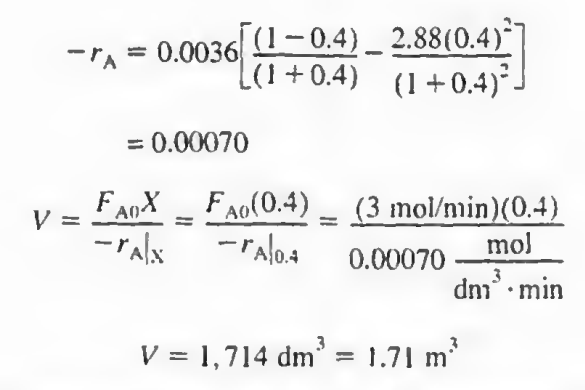
실제값은 1,714라고 한다. 대충 비슷하다고 치지 뭐~
이제 여기까지 왔으면 당신은 속도법칙을 아레니우스 식(k)과 농도의 항으로 표현할 수 있다. 이어서 화학양론표를 만들어 농도항을 전화율의 함수로 나타낼 수 있고, 이를 대입하여 반응속도를 전화율의 함수로 표현할 수 있다. 이후 예비 설계식

에 대입하고 적분하거나 레벤스필 도표를 이용하여 특정 부피를 구할 수 있다.
문제푸는데 필수적인 유용한 표를 첨부한다.
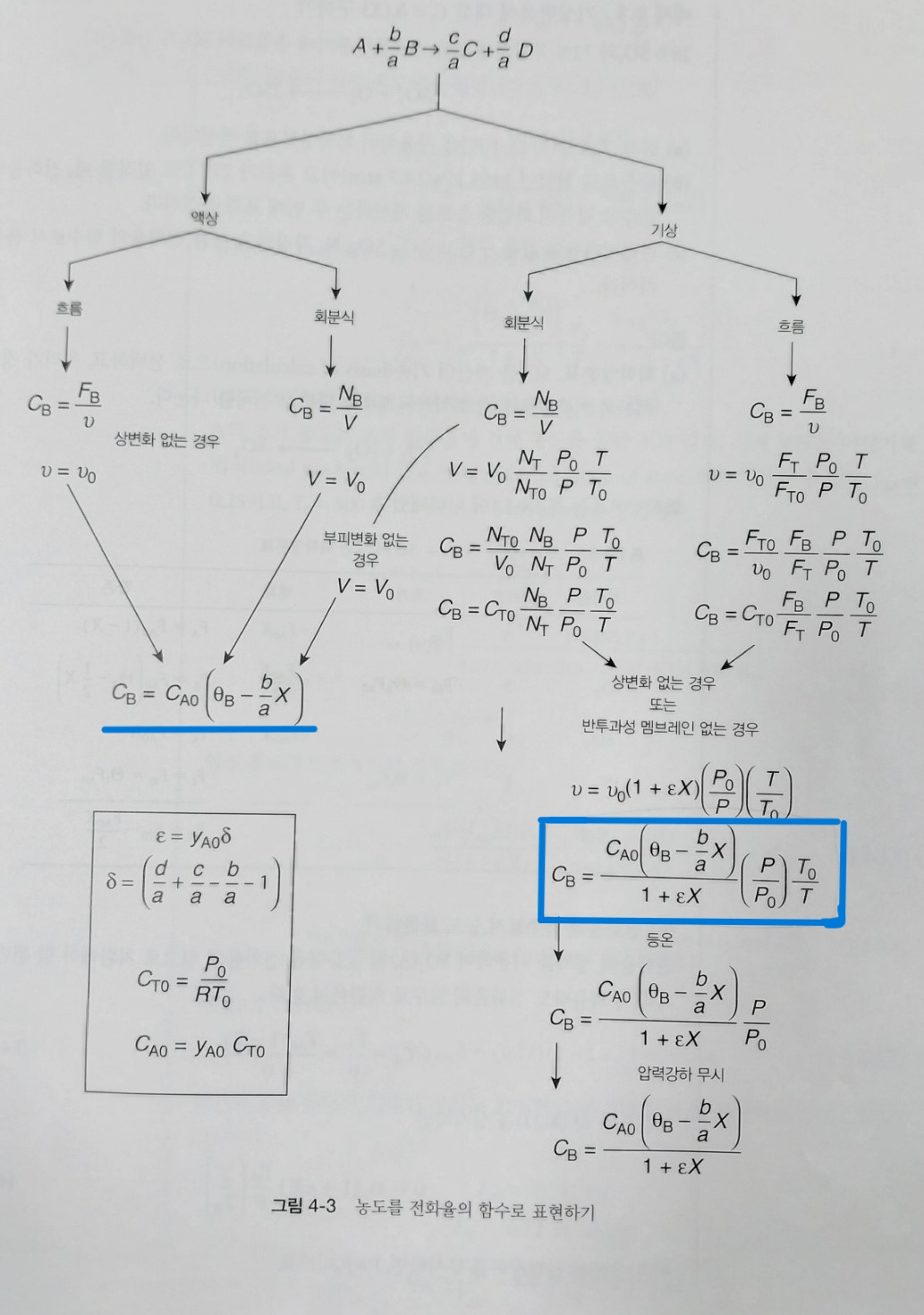
챕터4:등온반응기의 설계
먼저 등온 반응기는 온도의 변화가 없는 반응기이다. 사실 이전에 이미 배운 내용이지만, 설계체계를 다시 한번 살펴보자.

여기까지의 내용을 정리하면 다음과 같다.
ch4는 다음 장에서 알아보도록 하자.
'화학공학 일지 > 화학반응공학' 카테고리의 다른 글
| ch 10: 촉매반응과 촉매반응기 2 (3) | 2024.11.06 |
|---|---|
| ch10. 촉매반응과 촉매반응기 (1) (7) | 2024.11.06 |
| ch7: 반응 메커니즘, 생화학 경로, 생물반응과 생물반응기 (1) (5) | 2024.11.06 |
| ch5. 속도자료의 수집과 분석 (2) | 2024.11.06 |
| 화학반응공학 ch4: 등온반응기의 설계 (1) : 등온 등압조건에서 비가역 1차 2차 반응 (0) | 2024.10.08 |